Pythagoras
Neue Formeln zur Bestimmung
pythagoreischer Tripel
https://www.grin.com/document/1365537bzw.: Pythagoreische Zahlentripel und wie Formeln entstehen. Ein neuer Ansatz mit d = c - b - GRIN | Grin

Überblick zu:
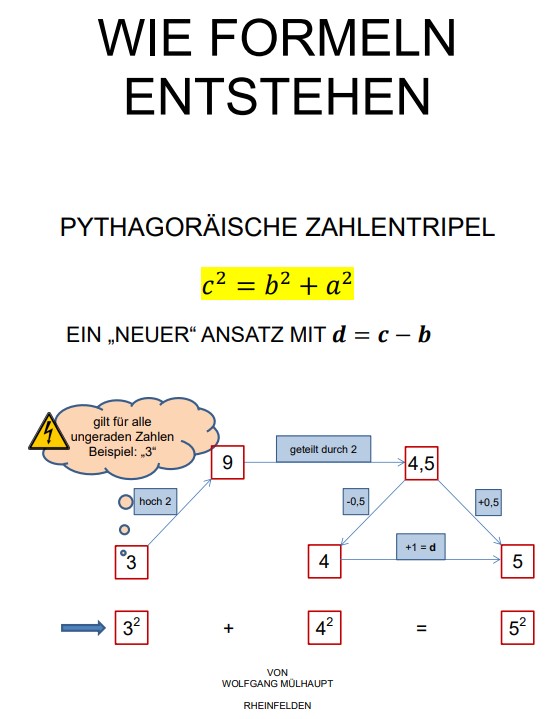
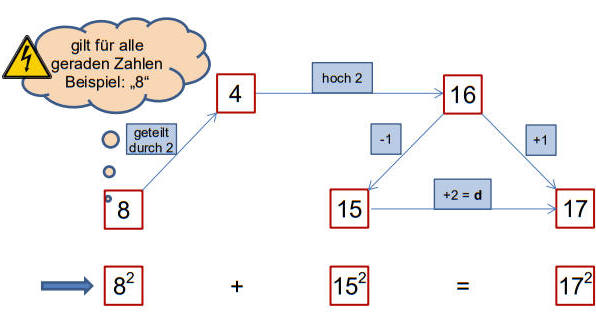
Pythagoräische Zahlentripel (c, b, a) - ein „anderer“ Ansatz mit d = c - b
Zunächst habe ich herausgefunden, dass c bzw. b abhängig von d mit einer quadratischen Funktion dargestellt werden kann.Bei der Variablen d muss unterschieden werden zwischen einer geraden Zahl und einer ungeraden Zahl, so dass man jeweils 2 unterschiedliche Funktionen erhält. Durch die Bestimmung von b wird dann c = b + d und anschließend a mit Hilfe des Satzes von Pythagoras gefunden.
Durch das Hinzunehmen der Variablen q wurden die fehlenden Lücken bei der Funktion zur Bestimmung von c bzw. b geschlossen.
Eine Herausforderung stellte das Finden der primitiven pythagoräischen Tripel dar. Dazu habe ich aus einer sogenannten Ausgangsfunktion Unterfunktionen bilden können, die nur primitive Tripel für c liefert. Dazu war noch eine Laufvariable i bei den Formeln nötig. Bei den Formeln spielte die Teilbarkeit und der ggT eine große Rolle.
Titelblatt von meinem Skript: